Dynamic symbolic execution

Abstract values

To begin with, let's see how we can create and manipulate symbolic values in Maat. A symbolic value is a value containing symbolic variables. Symbolic variables represent abstract data that has no concrete value on its own. They can be created with the Var() constructor:

from maat import *
m = MaatEngine(ARCH.X64, OS.LINUX)

m.cpu.rax = Var(64, "a") # Variable "a" on 64 bits
m.cpu.rbx = Var(64, "b") # Variable "b" on 64 bits

Just like concrete values in Maat, symbolic variables are Value objects and classical operators can be applied on them to create more complex expressions, as seen in previous tutorials:

>>> type(m.cpu.rax)
<class 'Value'>
>>> x = (m.cpu.rax + 0x100)*m.cpu.rbx + 2*m.cpu.rax  # Create a complex expression
>>> print(x)
((0x2*a)+((0x100+a)*b))
>>> type(x) # Combining variables with concrete integers still gives an 'Value' object
<class 'Value'>

Since symbolic variables don't have a concrete value, calling as_int() and as_uint() will fail on symbolic expressions:

>>> m.cpu.rax.as_int()
Traceback (most recent call last):
  File "", line 1, in 
RuntimeError: Cannot concretize symbolic variable without supplying a context

If we want to associate concrete values to the variables we can use the vars attribute of our MaatEngine, which is a VarContext object. This makes the symbolic variables become concolic, since they can now be concretized:

>>> m.vars.set("a", 0x12345678) # Set "a" to 0x12345678
>>> m.cpu.rax
a # RAX is still an abstract concolic value... 
>>> m.cpu.rax.as_uint(m.vars)
0x12345678 # ... but it can be concretized according to the symbolic variable context

# Note: for CPU registers only, the VarContext argument defaults to m.vars and can be omitted 
>>> m.cpu.rax.as_uint()
0x12345678

To summarize, we can have the following types of abstract values:

• concrete values: they contain no symbolic variables


• symbolic values: they contain at least one symbolic variable which doesn't have a value set in the VarContext. They can not be concretized and can also be refered to as 'fully symbolic' expressions


• concolic values: (concrete + symbolic) they contain at least one symbolic variable and all the variables it contains have a value set in the VarContext. They can thus be concretized

It is possible to check whether a value is concrete, concolic, or symbolic by using the is_concrete(), is_concolic(), and is_symbolic() methods:

# Constant value is always concrete:
>>> c = Cst(32, 0x1234)
>>> c.is_concrete(m.vars)
True
>>> c.is_concolic(m.vars)
False
>>> c.is_symbolic(m.vars)
False

# "a" is concolic when it has a value in the VarContext
>>> a = Var(64, "a")
>>> m.vars.set("a", 0x12345678) # Set "a" to 0x12345678
>>> a.is_concolic(m.vars)
True
>>> a.is_symbolic(m.vars)
False

# "a" becomes symbolic when its value is removed from the VarContext
>>> m.vars.remove("a")
>>> a.is_concolic(m.vars)
False
>>> a.is_symbolic(m.vars)
True

Making data concolic

To make a register symbolic, we can simply assign an abstract variable to it, just as shown previously:

>>> m.cpu.rax = Var(64, "a")
>>> m.cpu.rax
a   # RAX is now the symbolic variable "a"   

In order to make a register concolic, we simply have to save its concrete value in the engine's VarContext, before assigning the abstract variable:

>>> m.cpu.rax = 0x111 # Set some concrete value
>>> m.vars.set("a", m.cpu.rax.as_uint())
>>> m.cpu.rax = Var(64, "a")
>>> m.cpu.rax
a   # RAX is now the symbolic variable "a" 
>>> m.cpu.rax.as_uint()
0x111 # RAX can still be concretized to its concrete value

To symbolize data stored in memory, Maat provides the make_symbolic() and make_concolic() helper methods. They can be used as follows:

# Make memory purely symbolic
>>> m.mem.map(0x0, 0xfff)
# Symbolize memory at address 0x100 as an array named "buf" of 2 variables of 4 bytes each
>>> m.mem.make_symbolic(0x100, 2, 4, "buf")
>>> m.mem.read(0x100, 4)
buf_0   # Symbolic variable 'buf_0'
>>> m.mem.read(0x104, 4)
buf_1   # Symbolic variable 'buf_1'

# Make memory concolic
>>> m.map(0x0, 0xfff)
>>> m.mem.write(0x100, b'whatever') # Write concrete data
# Make memory at address 0x100 a concolic array named "buf" of 2 variables of 4 bytes each
>>> m.mem.make_concolic(0x100, 2, 4, "buf")
>>> m.mem.read(0x100, 4)
buf_0   # Symbolic variable 'buf_0'
>>> m.mem.read(0x104, 4)
buf_1   # Symbolic variable 'buf_1'

# The abstract variables context has kept the concrete memory values
>>> m.vars.get("buf_0")
0x74616877
>>> m.mem.read(0x100, 4).as_uint(m.vars)
0x74616877 # reading memory returns "buf_0", but it can be concretized
>>> m.vars.get_as_buffer("buf", 4) # Interpret 'buf_' vars as a buffer of 4-byte elements
b'whatever'

In addition to making memory symbolic, it is possible to generate standalone symbolic buffers with VarContext's new_symbolic_buffer() and new_concolic_buffer() methods. Those can be used to pass symbolic program arguments, or write symbolic data to the filesystem, as will be shown in a moment.

# Create symbolic buffer of 4 8-bytes values
>>> m.vars.new_symbolic_buffer("x", 4, elem_size=8)
[x_0, x_1, x_2, x_3]

# Create concolic buffer from a list of concrete values [1,2,3,4]
>>> m.vars.new_concolic_buffer("y", [1,2,3,4], 4, elem_size=8)
[y_0, y_1, y_2, y_3] # Returned buffer contains abstract concolic values...
>>> m.vars.get("y_0")
1 # ... so they can be concretized

# Create a concolic buffer of 1-byte values from concrete bytes
>>> m.vars.new_concolic_buffer("z", b'foo')
[z_0, z_1, z_2]
>>> chr(m.vars.get("z_0"))
'f'
>>> m.vars.get_as_str("z")
b'foo'

Solving symbolic constraints

Now that we have seen how to manipulate symbolic expressions and how to symbolize registers and memory, let's talk about constraints.

Constraints are instances of the Constraint class and represent arithmetic and logical constraints on expressions. Basic constraints can be built using all standard arithmetic comparison operators:

a = Var(64, "a")

# Create constraints
a == 100
a != 100
a < 100
a ≤ 100
a > 100
a >= 100 

Basic constraints can be combined with the built-in & and | operators:

(a == 100) & (a > 120)
(a < 100) | (a > 30)

Constraints can also be inverted by either using the built-in ~ operator, or by calling constraint.invert() (both are equivalent):

~(a == 100)
(a == 100).invert()

Great! Now let's see how we can solve constraints. Solving constraints means finding values for all the symbolic variables it contains so that the constraint becomes true. For instance, the constraint (a == 100) has only one solution for variable a which is 100. The constraint (a < 100) would have a 100 possible solutions for a (0, 1, 2, 3, ..., 99)

In Maat, constraints can be solved by using a Solver object. A solver can be created this way:

>>> solver = Solver()

Then constraints can be added with the add() method:

>>> a = Var(64, "a")
>>> b = Var(64, "b")
>>> c = Var(64, "c")

>>> solver.add(a > b)
>>> solver.add(b == c)
>>> solver.add(c == 0x42)

Once constraints have been added, we can try to solve them by calling the check() method. check() returns True if the solver could solve all constraints, and False otherwise:

>>> solver.check()
True

If check() was succesful, the solution to the constraint(s) (called a model), can be retrieved as a VarContext object with the get_model() method:

>>> model = solver.get_model()
>>> type(model)
<class 'VarContext'>
>>> model

a : 0x43
b : 0x42
c : 0x42

If we want to apply a given model to a current MaatEngine instance, we can use the update_from() method:

>>> m.vars.update_from(model)
>>> m.vars

a : 0x43
b : 0x42
c : 0x42
...

Finally, after solving the constraints, we can reset the solver and remove all the constraints it currently contains by calling reset():

>>> solver.reset() 

Cracking a basic challenge

Alright! We have learned everything we need about symbolic values and constraint solving and will now apply it on a concrete example. To conclude this tutorial, we will use Maat to automatically solve a simple crackme binary.

The challenge is called crackme1. Download it here (the archive contains the binary along with ld and libc libraries needed to load and execute it). The binary asks for a serial of 8 characters and will print Correct! only if the correct serial is entered:

$ ./crackme1 
Enter the 8-characters serial: abcdefgh
Wrong!

$ ./crackme1
Enter the 8-characters serial: ********
Correct!

Our goal will be to find out the correct serial. We could obviously solve the challenge without the source code, but to know what's going on let's take a glance:

// crackme1.c
#include <string.h>
#include <stdio.h>

unsigned long long transform(char* str){
    unsigned long long res = 0;
    for( int i = 0; str[i] != '\0'; i++ ){
        res = res << 8;
        res = res + ((str[i]*7 - 0x20) & 0xff);
    }
    return res;
}

int main(int argc, char ** argv){
    char serial[256];
    // Get serial
    printf("Enter the 8-characters serial: ");
    if( !scanf("%s", serial))
        return 1;
    if( strlen(serial) != 8 ){
        printf("Serial length must be 8\n");
        return 1;
    }
    
    // Check serial
    if( transform(serial) == 0x378ed80c535a3630 ){
        printf("Correct!\n");
    }else{
        printf("Wrong!\n");
    }

   return 0;
}

We can see that the source code doesn't contain directly the correct serial value. Instead, the user-supplied serial is processed by the transform() function which returns an integer computed from the serial (calling transform() with different serials will return different integers).

The integer returned by transform() is then checked against the hardcoded value: 0x378ed80c535a3630. If it is equal, the program deduces that the serial was correct.

Let's use Maat to automatically find the serial that makes the program print Correct!

First of all, we write a script that loads and run the binary. Since the program reads data from stdin with scanf, we will also add symbolic data in stdin (the symbolic filesystem will be explained in details in another tutorial, for now simply trust the example):

# solve.py
from maat import *
m = MaatEngine(ARCH.X64, OS.LINUX)
m.load("crackme1", BIN.ELF64, base=0x04000000, libdirs=["."])

# Fill stdin with 8-bytes concolic input
# Note: On a single-process linux environment, stdin handle is always 0 
stdin = m.env.fs.get_fa_by_handle(0)
buf = m.vars.new_concolic_buffer(
    "input",
    b'aaaaaaaa',
    nb_elems=8,
    elem_size=1,
    trailing_value=ord('\n') # concrete new line at the end of the input
)
stdin.write_buffer(buf)

Next, we will need to add hooks at the right place in order to find the input that makes the program print Correct!. To find the location we are interested in, we open the challenge in our favorite disassembler and find the branch that follows the input check:

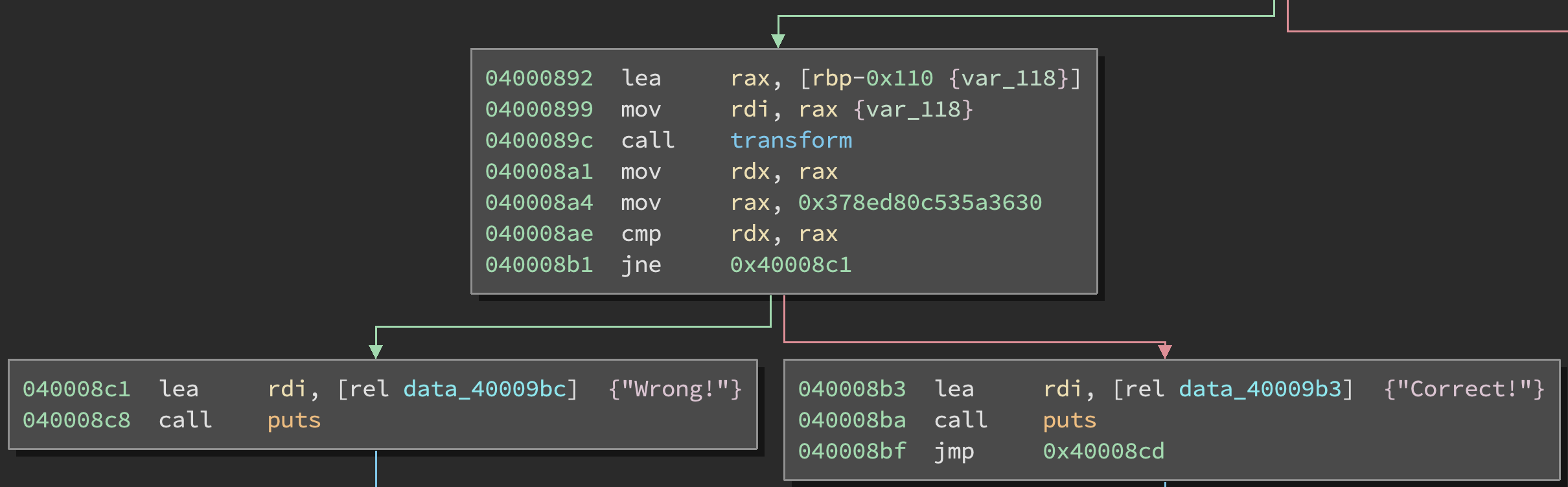
We see that the branch occurs at address 0x040008b1. Since the branch depends on the symbolic input, it corresponds to a path constraint. If you remember our previous tutorial, you know that we can hook the PATH event in order to instrument this symbolic branch. The goal is to get the branch condition, and then invert it so that we continue to 0x040008b3 instead of jumping to 0x040008c1.

As an exercice, try to write a PATH event callback that uses a solver to find an input that doesn't satisfy the branch condition. The solution is given below:

# <previous part of the solve.py script>

# Add hook on symbolic branch
def find_serial(m: MaatEngine):
    if m.info.addr == 0x040008b1: # We care only about that particular branch
        s = Solver()
        s.add(m.info.branch.cond.invert())
        if s.check():
            model = s.get_model()
            print(f"Found serial: {model.get_as_str('input')}")
        else:
            print("Failed to find serial")
        return ACTION.HALT
    
m.hooks.add(EVENT.PATH, WHEN.BEFORE, callbacks=[find_serial])

# Run analysis
m.run()

Running the entire script gives:

$ python3 solve.py
Found serial: 1bHt56z0

We can validate the solution:

$ ./crackme1
Enter the 8-characters serial: 1bHt56z0 
Correct!

We hope you enjoyed this introduction to dynamic symbolic execution. We showed how it can help to reason about potential user inputs and automatically find inputs that satisfy arbitrary runtime constraints. Of course we just scratched the surface of possible usage for symbolic execution, make sure to checkout our next tutorials to discover other applications and use-cases!